The Hungerford papers: playbook to break the teachers’ union
Get this Sierpinski triangle design on a PiFactory tee-shirt
PARKROSE school board — in collusion with Gresham-Barlow and Reynolds — appears to have been planning since 2009 for the chaos and mayhem that it unleashed on the communities this year.
When the boards claimed they were negotiating a new contract in good faith, it was not true. For a nearly a year they were not negotiating, they were following a playbook.
They were working to a game plan first mooted back in January 2009, and honed by January of this year into a playbook for the district superintendents to try to break the teacher unions.
Their goal was to raise up the administrators, including themselves,… but take back the middle-class family wagesand benefits as well as work-load protections districts had given to the teachers’ unions over the past five years or more.
The argument was that the economic climate made it an opportune time to cut back teacher pay and benefits and squeeze more out of teachers with bigger class sizes and more hours in the classroom… because teachers would never dare to strike.
It was at the 2009 winter conference of the Confederation of School Administrators (OACOA/OASE) that labor lawyer Nancy Hungerford presented her 12-page paper School District Options in Time of Financial Crisis. “Reopen the collective bargaining agreement (CBA) and reduce pay or benefits, with or without a reduction in work days,” headlined the opening section.
Classified staff as well as teachers — even former administrators — who have weathered this year’s board actions in Gresham, Parkrose and Reynolds will find paragraphs that ring alarmingly familiar in this three-year-old document.
The paper is a detailed review of case law plus legal options on how to navigate…
❏ introducing “re-opener” clauses,
❏ reducing the hours of classified staff,
❏ changing the length of the school year,
❏ exploiting changes in state funding in bargaining to cut pay and working conditions,
❏ timelines for declaring impasse,
❏ lay offs and how to to avoid Rif’d teachers from returning if jobs open up,
❏ how to use “competence” to replace experienced teachers with less experienced teachers,
❏ bargaining rollbacks,
❏ avoiding unfair labor practices…
❏ down to how to get rid of an administrator.
There is nothing here advocating anything illegal, or even sharp practice. Ms Hungerford and her brood are respected professionals. Rightly so. They could, and no doubt would, write you a detailed, strong brief on how to protect your rights at work against the school board… if you could afford them.
But school boards, with tax-payer dollars and arcane budget heads where spending can be hard to trace, can. And they do pay Ms Hungerford lots and lots of our dollars.
If you look at the Hungerford web site it is clear. The Hungerford family works for the employers. They offer advice, guidance and representation in:
❏ Evaluation, discipline, and dismissal of employees…
❏ Writing and administering plans of assistance for employees…
❏ Employer responsibilities under FMLA/OFLA/ADA…
❏ Non-discrimination and whistle-blower laws…
❏ Representation at the bargaining table…
❏ Interpretation of individual and collective employment agreements…
❏ Representation before the Employment Relations Board, Fair Dismissal Appeals Board, labor arbitrators, and in other administrative hearings…
❏ Representation in the Oregon Court of Appeals and Supreme Court…
❏ Representation in state and federal courts.
Ditto for college employers who want advice on student disciplinary procedures.
Then there’s advice regarding how to manage public meetings and public records issues, representation on ethics and open meetings law requirements, risk prevention recommendations, and so on. Look it up.
The Hungerford family also train senior district staff and administrators.
And, “New! A variety of services are now available to assist districts in negotiating, troubleshooting, and working collaboratively on an ongoing basis with charter schools.”
Ms Hungerford is the go-to lawyer if you are an employer. That’s simply what she does. We all have to make a buck. And that’s how Ms Hungerford and her kids make their buck, in the plural actually with lots and lots of s’s. School boards pay her their hidden tax dollars to work out how to screw — perfectly legally — their custodians, cooks, educational assistants, secretaries, teachers, counsellors, speech therapists, ELL specialists, bus drivers.
Three years ago it was lots of legaleze and small print.
Then son Brian put work in on Bargaining Trends and Bargaining Over Money in Difficult Times over 2010, fleshing out ideas about language, what words and phrases to go into a contract, what words and phrases must come out… from a district point of view.
He was less circumspect in his own language: On sacking “poor teachers,” for instance, “arbitrators are notoriously far less likely to uphold teacher dismissals… Nearly every arbitrator comes from a labor background, none have ever been in a position to have to deal with employee misconduct. The decisions of arbitrators cannot be appealed, no matter how ridiculous they are.”
The advice: “Districts should not, under any circumstances, agree to add back just cause for teacher dismissals.”
This year at the winter conference in the Salishan resort hotel at the end of January it was a powerpoint: New Challenges: Managing Labor, Employee, and Community Relations.
“Communities do not back increased salaries and insurance costs – and employees know it,” Ms Hungerford told her audience of school administrators. New Challenges was about the tactics for introducing the legal assaults mapped out in the previous couple of years.
Not only did they have the legal battlegrounds surveyed, they now had the plan of campaign, the logistics. What to do about a divided board, the chronic emailing parent, excessive public records requests, offensive threatening communications.
The Does and the Don’ts: Do avoid or eliminate any language that limits teacher evaluations. Don’t allow “just cause” as an appeal route for a dismissed teacher. Avoid limitations on measures of teacher effectiveness.
Can a position ever be filled with a new hire if employee on layoff not a “good fit” for opening?
Must added hours be given to classified employees who have lost hours?
When it comes to language, “less is best,” was the order of the day.
That was the playbook. The only problem, the teachers were willing to strike.
The Hungerford papers:
❏ Hungerford School District Options
❏ New Challenges: Managing Labor, Employee, and Community Relations
❏ Bargaining Over Money in Difficult Times
See also:
If I were the super…
What the school board could have done… In a nutshell they chose to divide our community when they could have chosen to unite the community.
Defend Parkrose schools — it’s about time
Get this Eratosthenes Net on a PiFactory tee-shirt
PARKROSE school board has not shifted its contract offer once in more than ten months. The Parkrose teachers’ union, the PFA, has made five significant moves to try to get an agreement on the teachers’ contract.
Now the board and superintendent have declared an impasse. Unless negotiations produce a settlement in the next few weeks, the board can unilaterally impose its final offer any time after Wednesday 11 April. Update: The board has issued a letter of intent saying it will impose its contract on Tuesday 17 April and PFA members have voted by more than 90% to give the authority for a strike Wednesday 25 April onwards.
The board’s contract will mean up to $1,200 a month less in teachers pay for the next six months plus between $300 and $600 less each month after that.
Of course, teachers are worried about such punitive pay cuts. They have families too. But the real fears are about how they can continue to do their jobs well and the future of education in Parkrose. Teachers’ working conditions are the learning conditions for students.
For the teachers it’s about time.
This year teachers agreed to a new schedule that increased their hours in the classroom by nearly 15% — nearly three weeks extra teaching time a year. The number of students teachers now see each day has more than doubled, up to 240 each day for some teachers. Class sizes have soared, some are now as high as 40+.
And time for daily preparation was cut in half, to less than 50 minutes.
On average teachers now have 56 seconds for each student each week in prep time. That to cover lesson prep, assessment, grading.
Because these schedules and prep cuts were imposed in September, the superintendent and board disingenuously and loudly claim their imposed contract will not affect teacher’s time. It’s only about greedy and selfish teachers wanting to take more cash they say.
Teachers’ workloads have gone up to make up for almost two dozen teacher jobs lost. Without the remaining teachers picking up that loss, many students could not now accrue the classes and credits needed for graduation. Teachers are more than doing their bit.
This year’s incoming freshpeople are going to struggle to graduate, simply by virtue of the fact that there are too few teachers to teach too few courses for them to get the requisite 26 credits. The arts and foreign languages have been particularly hard hit.
All this is causing serious stress inside the schools… for students as well as teachers.
The teachers’ union, PFA, wants to discuss workload issues. The teachers are particularly resentful of the increased form-filling bureaucracy insisted on by the superintendent, which seems more about the superintendent imposing her inflexible managerial will rather than helping teachers use valuable time efficiently.
Arrogant and pompous lectures by board members — particularly the board chair — about how to be a good teacher just exacerbate teacher frustration. Board members have barely spent hours let alone, days, weeks, months and years in the classroom.
The board and superintendent refuse to even talk about such issues, issues which seriously impact students. Ask your own student.
Teachers know school budgets are tight. That’s why last year the teachers agreed to ten unpaid furlough days — a 5% cut in pay — in a bid to keep teachers jobs. But the district still pink-slipped 13 teachers, including gutting another six from the high school.
This year teachers have offered a package that cuts their pay by up to $200 a month, with five days furlough this year and another six next year as well as changes to benefits packages.
But this is not good enough for the board and superintendent.
They also want to be able to tear up the contract any time and demand more cuts from the teachers… most likely more cuts in the school year next year but not excluding more pay and benefits cuts.
They claim there is no spare cash, period. But the audit and small print show there is enough to fund the difference between the board’s proposed punitive pay cut for teachers and what would still be a substantial pay cut for teachers, but a pay cut that teachers and their families can survive.
More than $2.2 million in the budget is unassigned. A further staggering $0.5 million is assigned to teacher early retirement, to cover the unlikely event that all those who could qualify for early retirement will all apply in one go. And there appear to be bits and pieces salted away in other budget heads. And for the past years the board has always spent short of its budget as every final audit — including this year’s — shows.
Teachers are not saying those sums should be assigned to their pay, far from it: but it is possible for the board to negotiate and move to make bearable the pay cut the teachers have said they will take. $400,000 is the difference between the survivable pay cut put forward by the teachers and the punitive pay cut demanded by the board and superintendent.
After all, there is enough money to fund a $7,000 rise for the superintendent, taking her total package to some $170,000 a year, $30,000 more than that of Sam Adams, mayor of the city of Portland.
And while teachers jobs have gone from the Parkrose classrooms — 23 in the past three years — jobs have been added in the superintendent’s district office.
This rigid and vindictive attitude by the superintendent and her board seems to indicate there is more to this year’s negotiations than meets the eye.
The reality is the school board and superintendent are exploiting the budget crisis to go much further than just balancing a budget. They are using the budget crisis, shock-and-awe, to destroy the teachers as a collective body, destroy their union. Inevitably this must undermine teaching and real education for school students in Parkrose.
What the board wins now, it has no intention of giving back later. Its proposed cuts and imposed working conditions — for students as well as teachers — inside the schools will be permanent.
When school funding eases the school board will not come back, saying words to the effect of, hey guys, thanks, let’s talk.
As the board chair angrily told PFA negotiators — when no members of the public were present — the board simply thinks teachers are overpaid. And that’s what it’s about. Cutting teachers down to low-paid classroom operatives. The result will be a dumbing down of public education in Parkrose, lessons and student support reduced to the lowest rote common denominator.
This is about cynically using a real budget crisis to tear apart teachers’ pay and working conditions, and emasculate the union as a credible negotiating partner. For ever… or, at least the next decade.
There are clear signs that the board is working in collusion with the neighboring Gresham-Barlow and Reynolds school boards to undermine all teachers across the East County. The aim appears to be to gut the Oregon Education Association in the East County area.
Gresham-Barlow school board has voted to impose its teacher-busting contract on 22 March and Reynolds is expected to declare impasse shortly. The three boards are coordinating their timetables to weaken the impact of any teacher strikes. Teachers need to give ten days notice of strike action.
Whether or not it is the intention of individual board members, their version of the contract will further reduce the student experience in Parkrose to the lowest test-based production line. The actions of the board and superintendent will make teaching in Parkrose become a low-low middle class job, not even a profession. And the result will be to make education even more a mechanical chore for the students.
Planned creative lessons will give way to whatever can be scrambled together, focusing on test needs. If senior experienced teachers retire early, so what? After all, there’s lots of young, eager new graduates willing to take low-paid jobs. Why pay experienced teachers? Why, even, encourage or help young teachers become experienced teachers?
Gresham-Barlow is imposing a contract that allows it to get rid of experienced teachers in favor of lower-paid, inexperienced teachers.
The boards just need cheap, licensed warm bodies to stand at the front of overcrowded classrooms teaching to the test. It’s the test numbers they follow. And when they go up — which they have — the Parkrose board passes a resolution congratulating… itself!
The Parkrose board clearly signaled its attitude when it slashed the working hours and conditions of the Parkrose classified staff — custodians, educational assistants, admin staff — cutting benefits and pay to poverty levels. And leaving the most vulnerable students without the full support needed.
The superintendent’s increasingly outdated autocratic, mechanical and bureaucratic management style — modeling her much-touted need for collaboration by refusing to collaborate with her own staff — points to a fundamental lack of inspirational vision, a future of Parkrose schools staffed by low-paid teachers working at a level barely above test-prep crammers.
Large class sizes, rote lessons, little support, oppressive demoralizing management, teaching to the bureaucratic form and mechanical decree, all-important tests, bewildered and uninspired students. Factories, not schools.
Please show support by liking Parkrose Faculty Association on facebook.
The PFA web site is at parkrose-faculty.org
Follow twitter.com/parkroseteacher for updates of teacher actions
Follow me on twitter.com/pifactory
How to think like a mathematician
Buy this Sierpinski triangle design on a PiFactory tee-shirt
REAL mathematics develops by stumbling forward, and occasionally backwards. Take a problem, try to solve it, reflect on what you’ve learned and then change the problem and try again. Heuristics. It’s not how the math textbooks present the subject. So, how to give kids a feel for thinking like a real mathematician? And gaining the confidence to think like a mathematician?
As this simple problem (taken from Reardon Problem Solving available from www.as.ysu.edu/~thomasr/pss.htm) seemed to have worked, it’s worth sharing.
As we started I emphasized the aim was for all students to feel how it feels to think like a mathematician: We were going to do a simple problem, focus on what it feels like and what we did… and then change the problem and try again.
The problem: Take the sequence 1, 2, 3, 4, 5 and five circles arranged in a cross — with one circle in the center and two circles top and bottom and two circles either side. Place each number in a circle such that the sum of the numbers in the circles across equals the sum of the numbers in the circles going down.
I asked my classes to try it out and emphasized I wanted them to remember their first thoughts on tackling the problem.
Before I had finished introducing the problem hands were going up with students proudly declaring “done!” and sitting back with an answer on their paper. I asked a student to put up their answer. Immediately another student announced they had a different answer. And then a third, yet another answer. I asked if there were a fourth? With no takers, I asked students to recall their first thoughts.
“I took 1, 2, 3, 4 and put them in the outer circles and then the 5 in the center, and went from there.”
“I knew the sums couldn’t be more than 10, so I opted for a sum of 8 and made it work.”
“I just put numbers in the circles till it worked.”
“I spotted 4 + 1 and 3 + 2 both equal five, so I put the 1 in the center.”
“I’m hungry… no, I mean, I put the biggest number in the center .”
So, I pointed out, there’s at least three answers. And different students seem to have had different thoughts about how to start. Remember, in group work different students will have different approaches. We agreed the first attempts were starts to guess and check.
Then we looked at the three answers on the board. Can you spot any patterns? I prompted. After an initial silence and a few stabs along the lines of the 1 and 5 always fall in the same line of circles, the focus was on the the number in the center circle. Students described the numbers variously as “odd”, “not-even”, or the “first, middle and last numbers”. Someone pointed out the totals were 8, 9 and 10. The sum of the top and bottom numbers must equal the sum of the two side numbers another pointed, leading a discussion that focusing on the outside numbers also gave clues.
Ok, now try 2, 3, 4, 5 and 6.
The response was quicker. And most students now carried on after finding one solution. Students put answers on the board. First thoughts included, “I went for the odd numbers in the center, but there were just two, so I put the even numbers in the center circle”.
“I looked for pairs of numbers that had the same sum.”
“I looked for the first, middle and last numbers and put them in the center circle.”
So, is there a fourth solution? I asked pointing back to our first list of 1, 2, 3, 4, and 5. Students seemed confident there wasn’t. Explanations focused on putting an even number in the center circle: there was then no way the four remaining numbers could be paired to give equal sums, or, the sum of the remaining numbers was odd and could not be divided by 2.
So, will it work for any set of five consecutive numbers (we played hangman to get the word “consecutive”)? Yes, was the consensus. Students tried with their own numbers. Examples gave sums of tens, hundreds and even thousands, but with all students able to experiment with their own sequence. By now some students were branching out: It works for 30, 45, 60, 75, 90 said one (do they have common factors I suggested). Can we use decimals? asked another. What about negative numbers? another ventured.
We summarized: If the first five numbers we looked at had been one of the latest student-generated examples, we’d have all got stuck and would have given up, I suggested. We went simple, guess and checked, learned from that, changed the problem and tried again using what we’d learned from our first try. And again.
OK, does it work for any consecutive five numbers? Yes most agreed. But, bearing in mind this is an algebra class, how can we prove it?
After a bit of prodding, x was suggested. Variables someone else explained.
Looking back to 1, 2, 3, 4, 5 what if x =1, how would we write 2? I asked. y? said one student. z? another.
Getting to (x + 1) didn’t come immediately. But (x + 2) came tumbling out once that obstacle was surmounted followed by (x + 3), each written below the appropriate digit 1 through 5. Now, the problem was to find three solutions for the consecutive sequence of x, (x + 1), (x + 2), (x + 3) and (x + 4). Use what you’ve learned I suggested.
For some students this was a struggle, though most seemed to be able to follow along and find a second solution once a member of their group cracked it and gave one of the three solutions.
Meanwhile, one student was changing the operation from addition to multiplication and another had expanded the sequence to nine numbers and circles. You can make it work he proudly announced.
Engaging math for all learners
Buy this Eratosthenes Net on a PiFactory tee-shirt
The UK extends its revised secondary (high school) national curriculum to 15-year-olds from September. The focus is on engagement, and in particular engaging all learners — regardless of ability — with rich, varied and compelling math activities.
And to reflect the new priorities, the UK’s public examinations — the General Certificate of Secondary Education GCSE — will boost assessment of applications and problem solving from 20 per cent to 50 per cent.
“This does not mean that technical competence is no longer important, rather that just being able ‘to do’ mathematical techniques will not be sufficient,” writes Sue Pope of the UK Qualifications and Curriculum Development Agency* in Mathematics in School.
“Students will need to be able to think for themselves and decide when and how to use their mathematics to tackle problems within mathematics and in other contexts.”
The new curriculum is ambitious and defines “an entitlement of experience for all learners.
“Rather than labelling learners and restricting access, the richness of the entire progamme of study needs to be made available to all,” says Sue Pope. “Whilst this may seem daunting, particularly if you are used to teaching level by level… it can also be liberating.”
Mick Waters, director of Curriculum at te QCDA: “If we want young people to do well in mathematics, it helps if they enjoy the subject… to see that the subject is fascinating and exhilarating, to see the way it affects everyday life and helps to change the world in which we live.
“We have to strike a balance between the challenge of incremental steps in understanding, knowledge and skills, and the joy, wonder and curiosity of learning.
“It is not about ‘basics’ and ‘enrichment, all children should have a rich experience.”
For students to develop problem-solving and mathematical thinking schools “their classroom experiences need to be rich and varied”:
A rich mathematical task…
❏ Engages everyone’s interest from the start,
❏ Allows further challenges and is extendable,
❏ Invites learners to make decisions about how to tackle the activity and what mathematics to use,
❏ Involves learners in speculating, hypothesis making and testing, proving or explaining, reflecting, interpreting,
❏ Promotes discussion and communication,
❏ Encourages originality and invention,
❏ May contain and element of surprise,
❏ Is enjoyable,
❏ Allows learners to develop new mathematical understandings.
The QCDA worked with some 30 UK schools to develop programs of rich tasks aimed at “combining understanding, experiences, imagination and reasoning to construct new knwledge”.
Tasks and case studies are spelled out in the downloadable Engaging Mathematics for all Learners.
*Shortly after the election of a new Conservative government in May, the UK Department of Education announced legislation will be introduced in the autumn to close QCDA.
A picture is worth a thousand calculations
Buy this Sierpinski triangle design on a PiFactory tee-shirt
BREANNA is a quiet student who patiently sits in my math class waiting for the ordeal to end. She is too polite to complain or cause a fuss or disturb any of her peers with disruptive behavior.
She does take some notes, and with encouragement will attempt some of my questions. But, to be frank, Breanna gets almost nothing from my math class, apart from sitting through a course she needs on her transcript to walk the walk.
Breanna’s passion is drawing, mainly caricatures heavily influenced by animé. She is good, very good. Tucked under the notebook for my class is her pad. As token gestures go into her math notebook, a detailed and dramatic picture builds unseen on her pad.
When we did our Pascal’s triangle and binomial theorem investigation and poster
Blaise Pascal by Breanna
Dutifully she showed me her growing list of artists and I eagerly awaited which one she would choose… Vasarely, Riley, Mondrian… hopefully not Escher.
Is it OK to look at pyramids? she asked. The proportions are interesting she explained.
Since her math notebook — not her art pad — has added calculations about the angles and proportions of the Gizza Great Pyramid and neighbors. Was it OK to look at less famous pyramids asked Breanna.
Her self-selected extension was to find some more obscure pyramids and compare the proportions.
Then came the poster, with a giant yellow pyramid, drawn to the correct proportions.
❏ For me, the value of this project was that Breanna did some mathematical thinking, where before she was doing none, other than sitting through a curriculum that had little interest, meaning or use for her.
It was also interesting to see that simply giving Breanna the freedom to pursue some mathematics of her own choice based on her own interests did indeed lead to some mathematical work.
What was surprising was that Breanna didn’t choose an overtly artistic piece of mathematics, such as a painting influenced by geometrical shapes. Though, in Breanna’s eyes a Pyramid is a piece of art.
Tilting towards Nrichment
Buy this Eratosthenes Net on a PiFactory tee-shirt
TILTED SQUARES from the inspirational UK site nrich.maths.org is a great example of an open-ended math problem that leads to some deep math thinking… even among students who don’t normally show much interest in their math lesson.
The task at first sight appears to be quite simple. A square drawn on square-dotted paper is tilted by raising the lower right-hand corner vertically by one dot, and a new square is then drawn on this tilted base. The question is, what is the area of the new square? And then, is there a pattern to the areas with continuing tilts, as the lower right-hand corner is raised by a dot at a time? The immediate response of almost all the students in my classes was, the first square and the second square were exactly the same. This, even from my most accomplished mathematical thinkers. The Nrich site has an interactive program, so the square can be repeatedly tilted and projected. Even on tilt three or four students were still insistent the areas remained the same. Only when the square had tilted to become what students call a diamond, was there questioning.
My two most inquisitive students held out until after they’d carefully drawn and cut out the first two squares and placed one on top of the other before they would countenance any change.
Problems from Nrich seem to self-differentiate: two students who rarely are able to engage in more traditional exercises, quickly constructed on dotted paper a pattern of 18 tilted squares. They were excited. They were animated. And they wanted to talk about, and show what they had done. Others insisted on constructing the pattern on the interactive whiteboard. They did this while some of my more “analytical” students struggled to visualize and draw the squares, unable to identify the corners of a newly-tilting square.
Some students explored finding the areas of the square by measuring, and others tried Pythagoras.
The first found the results frustrating as they estimated fractions of a millimeter change in length, squaring the answers and ending up with lots of decimals and no clear pattern. The Pythagoreans built up tables and areas and tried to spot a pattern in the growth. They quickly spotted a pattern which they could verbally explain and extend, but could not or would not commit their analysis to paper, other than to list the answers.
Students were encouraged to try with a differently-sized first square. With a smaller starting square, the growth in area is more quickly apparent. The Pythagoreans could verbally list the areas with ease. But they refused to countenance any search for a method that could be committed to paper.
The majority drew several squares, and tried to estimate the area by counting squares formed by the dots — or just counting dots as an estimate. They could not extend to the results of the Pythagoreans, but were much more open to watching some hints on the interactive whiteboard: Why not a square with a horizontal base around the outside of any tilted square?
The area of the outside square, subtract four triangles and you have the area of the tilted square. The visual approach appealed to our early pattern artists, and provided the clue for the majority who were searching for a calculation.
Quickly more areas were forthcoming, while the Pythagoreans reluctantly drew some titled squares with exterior square… only to dismiss the approach with open scorn.
What if there are 99-tilts? The Pythagoreans raced for the answer, but could not agree.
Meanwhile another hint: Build up a table breaking each area calculation down into all of its detailed parts, including some reference to the tilt number. Use different colors for the numbers from different parts of the calculation, red for the tilt number, green for the side length of the outside square and so on. Is there a pattern?
What if the tilt number is n, representing the nth tilt? Can n be identified in the pattern?
The early doubters confidently give the answer for the area of the 99th tilt. The Pythagoreans are still arguing about the mental math, though there are signs on paper of the formula that was, indeed, in their heads.
And the artists had now produced colored titled squares and were demanding their works were now put on display.
Now that’s enriched mathematics. And nothing feels so Good!
❏ For more discussion about using open-ended questions to promote mathematical thinking… plus thoughts on what exactly constitutes math thinking see About Nrich: research plus articles
The elephant in the classroom
Buy this Mathematicians have Great Powers PiFactory tee-shirt
JO BOALER’s research into what works and what doesn’t inside a math classroom has gone a lot further than just watching, literally, hundreds of math classes. She has tracked down the pupils she’s observed years later as adults and quizzed them on how their experiences in the classroom prepared them for using math in real adult life.
Her findings show not only how badly wrong the still dominant, traditional style of math education can be… but how it is possible to turn the situation around, that a growing number of schools are finding ways to engage students in deep math thinking that lasts for life. And gives pleasure.
Open-ended problem solving, mixed-ability group work and project work as well as lots of discussion apparently can unlock the hidden mathematician in every child. Of course, avoiding the superficial quest for educational silver bullets, the real implications for pedagogy in the classroom go much further.
“There is often a very large elephant standing in the corner of maths classroom… the common idea that is extremely harmful to children is the belief that success in maths is a sign of general intelligence and that some people can do it and some people can’t.” says Jo Boaler in the introduction to The Elephant in the Classroom, Helping Children Learn and Love Mathematics*.
“Even maths teachers (the not so good ones) often think that their job is to sort out those who can do maths, from those who can’t. This idea is completely wrong…
“In many maths classrooms a very narrow subject is taught to children, that is nothing like the maths of the real world or the maths that mathematicians use (PiFactory emphasis). This narrow subject involves copying methods that teachers demonstrate and reproducing them accurately, over and over again. Of course, very few people are good at working in such a narrow way…
“But this narrow subject is not mathematics, it is a strange mutated version of the subject that is taught in schools.
“When the real mathematics is taught instead — the whole subject that involves problem solving, creating ideas and representations, exploring puzzles, discussing methods and many different ways of working, then many more people are successful.”
Boaler calls it a classic win-win: “teaching real mathematics, means teaching the authentic version of the subject and giving children a taste of high-level mathematical work, it also means that many more children will be successful in school and life.”
+++
Boaler followed classes in two schools in the UK for three years, and then interviewed former students almost a decade later in their mid-20s. One she calls pseudononimously Phoenix and the other Amber Hill.
At Phoenix the teachers adopted what they called “a project-based approach”. Instead of teaching mathematical procedures, students from age 13 worked every day on open-ended projects that needed mathematical methods.
When Boaler asked Phoenix students what to expect, the responses were “chaos”, “freedom…” Boaler confirms the “classrooms at Phoenix did look chaotic”. The project approach “meant a lot less order and control than in traditional approaches”.
A typical project was Volume 216 — an object has a volume of 216, what could it be, what would be its dimensions, what would it look like?
At Amber Hill classrooms were quiet and peaceful. Teachers began lessons by lecturing from the board, followed by students working through exercises. Students worked quietly, mostly in pairs. They could check answers with each other, but they were not encouraged to discuss their mathematics.
At Phoenix a student described activity in the classroom: “You’re able to explore, there’s not many limits and that’s more interesting.”
An Amber Hill student: “In maths, there’s a certain formula to get to, say from a to b, and there’s no other way to get to it, or maybe there is, but you’ve got to remember the formula. In maths you have to remember, in other subjects to you can think about it.”
At age 16 all the students sat the UK’s major three-hour public GCSE mathematics exam. Although the Phoenix students had tested lower than the UK national average before their project-based lessons started, their GCSE grades were significantly higher than Amber Hill’s and the national average.
But it is the achievements and recollections of the students nearly a decade later that speak more powerfully. Boaler recorded her research more fully in the national book award winning Experiencing School Mathematics.
At school all the students were in similar social class levels, as defined by their parents’ jobs. Eight years later more than six out of ten of the Phoenix students had moved into jobs that were more highly-skilled or more professional than their parents. The figure for the Amber Hill students was less than one-in-four. Over half the Amber Hill students had lower-skilled jobs than their parents, the figure for Phoenix was less than one-in-six.
Looking back to his school years, Phoenix student Paul said: “I suppose there was a lot of things I can relate back to maths in school. You know, it’s about having a sort of concept, isn’t it, of space and numbers and how you can relate that back… maths is about problem-solving for me. It’s about numbers, it’s about problem-solving, it’s about being logical.”
Marcos from Amber Hill said: “It was something where you had to just remember in which order you did things, that’s it. It had no significance to me past that point at all — which is a shame. Because when you have parents like mine who keep on about maths and how important it is, and having that experience where it just seems to be not important to anything at all really. It was very abstract. As with most things that are purely theoretical, without having some kind of association with anything tangible, you kind of forget it all.”
Boaler also worked closely with in an inner-city high school in California called Railside. There teachers who had originally taught using traditional methods with classes grouped according to notions of ability focused instead on mixed-ability groups and a re-designed curriculum built around big mathematical ideas.
Instead of an approach based on isolated skills and repeated practice, the Railside students worked on themes — such as What is a linear function? — using multiple representations, the different ways maths could be communicated through words, diagrams, tables, symbols, objects and graphs.
Again Railside was monitored alongside schools adopting a more traditional approach. Although Railside students started with lower levels of achievement, after two years they were outperforming the other schools. By year 12, more than four out of ten Railside students were in advance classes of pre-calculus and calculus. The corresponding figure for the more traditional schools was fewer than on in four.
The four-year study at Railside revealed consistently higher levels of positive interest in mathematics at Railside.
At the end of the study only 5 per cent of students from the traditional schools planned a future in mathematics. At Railside the figure was 39 per cent.
Janet: “Back in middle school the only thing you worked on was your math skills. But here you work socially and you also try to learn to help people and get help. Like you improve on your socialskills, math skills and logic skills.”
Jasmine: “With math you have to interact with everybody and talk to them and answer their questions. You can’t be just like ‘oh here’s the book, look at the numbers and figure it out.’
“It’s not just one way to do it… it’s more interpretive. It’s not just one answer. There’s more than one way to get it. And then it’s like: ‘why does it work?'”
Jo Boaler concludes: “Put simply, because there were many more ways to be successful at Railside, many more students were successful.”
Eight key questions for teachers and parents:
❏ Is our school’s mathematics approach teaching children to think and reason and make sense of the mathematics they are learning?
❏ Is practice with skills provided in engaging, challenging and mathematically important contexts?
❏ Is persistence valued over speed?
❏ Are problem solving and the search for patterns at the core of all that children are asked to do?
❏ Is numerical reasoning emphasized?
❏ Does the mathematics approach emphasize that there is almost always more than one way to solve a mathematics problem?
❏ Does it present mathematics as relationships to be understood rather than recipes to be memorized?
❏ Are children the ones who are doing the thinking and sense making?
+++
* The Elephant in the Classroom, Helping Children Learn and Love Mathematics will be published in March in the UK. An earlier account of Boaler’s research is available in the US entitled What’s Math Got To Do With It, how parents and teachers can help children learn to love their least favorite subject, and why it is important for America
Lakatos, the Jack Kerouac of math
Buy this Sierpinski triangle design on a PiFactory tee-shirt
“WHEN will I need any of this in real life?” is such a common question in a math classroom that it is a cliché.
At one level it is a tried and tested way to stop a lesson. At another it is a genuine question. After all, if a student isn’t going to use the likes of the Quadratic Formula, why learn it? And spend so much time, over so many years, learning it all? And suffer so much stress1? Why, indeed, does an average student need much more than the numeracy required to navigate life?
The question does not come so often from the student who enjoys math, which also usually means the student who is more than competent at it.
The answer used by myself, and some other teachers I know, is that math is about creative thinking skills, and, going further, the ability to think in abstract terms, to examine problems from different perspectives, the bending of minds. The other oft-used term is problem solving. Problem solving, creative and logical thinking skills are essential life skills.
Some look convinced.
Those who don’t need to ask the question (but may out of genuine, disinterested curiosity) carry on, almost entirely driven by their own motivation.
The question facing math educators is how to make math relevant — and fearless — for the rest?
Students may not need, or ever use, the Quadratic Formula, but finding the Quadratic Formula with the aid of algebra tiles, completing the square and computer manipulatives as well as some help from other students does need skills that are useful for life… the sort of math thinking skills needed in an increasingly complex technological world… an increasingly complex political, economic and social world.
Proofs and Refutations, The Logic of Mathematical Discovery by Imre Lakatos raises not just a question of how math is taught. It is also raises questions that go to the core of what education is about. Like the world, it is complex, technological, social and political in nature. There are many stakeholders, besides the students.
The pressures on teachers (and students) are contradictory.
The modern math teacher is meant to create rigorous, interesting, relevant, fun, diverse, engaging, multi-cultural, technology-based, investigative lessons that allow each student to search out their own path of discovery, at their own pace, based on their independent learning plan in co-operative group situations tailored to each student’s own learning style.
At least three times a day.
Plus relevant daily assignments with meaningful and timely, individualised feedback. Fully covering the curriculum. And preparing the student for repeated, on-the-record, high-stakes, multiple-choice computer testing… the results of which are the meat for the political-funding grinder.
So. No pressure then.
Teachers and students find themselves caught between the traditional deductivist approach and the vision of an heuristic future.
The demands of the curriculum, rigorous testing regimes, daily assignments, textbook styles and time all push the teacher back in the direction of deductivism. And as most parents are the product of deductivism, they too are fans— even while assuring the teacher they themselves hated math at school.
Competition from new interactive media, educational research and sheer desperation and frustration push the teacher to at least dream of an heuristic world where students are engaged and thinking for themselves.
Lakatos could easily have chosen a different title for this delightful read: Proofs and Refutations, the Heuristic of Mathematical Discovery.
Here Epsilon, Pi, Omega battle it out with Alpha and Beta: Adventure and the search for knowledge versus battalions of formalists, logical positivists, conceited infallibilists, dogmatists, Euclidean rigourists, monster barrers.
In the final few pages2 Lakatos abandons his pseudonymous allies and speaks directly with Shakespearean passion, anger and open contempt for the deductivist approach.
Lakatos summarises this “Euclidean ritual” as painstaking lists of axioms, lemmas, unseemly definitions followed by carefully worded theorems, often loaded with heavy-going conditions. The theorem is followed by the proof.
“The axioms and definitions frequently look artificial and mystifyingly complicated.”
The student of mathematics is obliged “to attend this conjuring act without asking questions either about the background or about how this sleight-of-hand is performed.” Should a student wonder or discover by chance that mathematics could not have developed in such a fashion, “the conjuror will ostracize him (sic) for this display of mathematical immaturity.”
Lakatos complains, “mathematics is presented as an ever-increasing set of eternal, immutable truths.
“Counterexamples, refutations, criticism cannot possibly enter.” Conjectures are suppressed.
This “authoritarian” deductivist style “hides the struggle, hides the adventure.
“The whole story vanishes, the successive tentative formulations… are doomed to oblivion while the end result is exalted into sacred infallibility”.
And then the coup de grace buried in the footnote (p142, n2): “It has not yet been sufficiently realised that present mathematical and scientific education is a hotbed of authoritarianism and is the worst enemy of independent and critical thought.”
In contrast Lakatos models a more open and optimistic approach, a world where imperfection is a virtue. For Lakatos it’s not the answer that counts: it’s how you get an answer, which only leads to the next question, that matters. Learning as a journey. And it’s the road that’s interesting, not so much the destination… which is only a starting point of another road.
Lakatos is the Jack Kerouac of mathematics.
“Literary criticism can exist because we can appreciate a poem without considering it to be perfect; a mathematical or scientific criticism cannot exist while we only appreciate a mathematical or scientific result if it yields perfect truth.”
Lakatos has not yielded perfect truth. But this work helps put us on a road of discovery in the classroom. For Lakatos education was about fostering independent and critical thought, and for him that would mean adopting the road of discovery and not the Euclidean ritual – “this good and evil spirit of nineteenth century mathematics”.
But Lakatos was a political man3. And much of Proofs and Refutations has the passion of a revolutionary political manifesto.
Lakatos would have recognized the tensions and politics that mire modern-day teaching.
On the one hand: open-ended investigations, discovery, problem solving and self-learning, assessment for learning. The heuristic method.
On the other: the insistent political pressure of test scores, pushing teach-to-the-test strategies. The rigidity of the curriculum map. Students trained to view education as a production line for collecting points. Assessment of learning. (Assignments means points. Tests means points. And as the most amusing, satirical show on BBC radio4 for many years always said, “points means prizes…” Grades, GPAs, scholarships, college, career.)
But there is a synthesis out of this Euclidean thesis and heuristic anti-thesis. Behind the closed doors of classrooms teachers are experimenting with counterexamples and stretching concepts to open up new conjectures5 which may yet give greater depth and breadth to real learning.
+++
1 I did a Google search some time ago for “math phobia”. It returned 527,000 links. I put the same words into amazon.com and a list of 234 self-help guides was returned with names such as Overcoming Math Anxiety, Conquering Math Phobia: A Painless Primer, Danger Long Division, Overcome Your Math Phobia and Make Better Financial Decisions. And many, many more.
2 Lakatos puts clues in his opening pages. Heuristics is mentioned in both the Acknowledgements and the Author’s Introduction. And in the opening pages Lakatos teasingly makes clear, in a lengthy footnote (p9), that for pre-Euclidean Greek mathematicians porisms, results that appeared by chance, springing from the proof of a theorem, were considered a windfall, or bonus. “The heuristic precedence of the result over the argument, of the theorem over the proof, has deep roots in mathematics,” says Lakatos. As the mathematicians in Lakatos’ sites often pointed back to some notion of a golden age of Greek mathematics and rigid method, this Lakatos footnote is an opening salvo.
3 Lakatos was a member of the Hungarian Communist Party and an active member of the anti-fascist armed resistance during the Second World War. After the war he was a part of the Communist administration and was involved in the reform of Hungarian higher education. He spent six weeks in solitary confinement and three years in prison. The reasons why are unclear— He was rehabilitated in 1953. After Lakatos fled Hungary and the Soviet invasion of 1956 he was supported by the Rockefeller Foundation and the London School of Economics. At LSE he remained a close friend and colleague of Georgy Lukacs, widely accredited as the father of western Marrxism. He also befriended Paul Feyerabend who formulated an anarchic theory of knowledge.
4 I’m sorry I haven’t a clue, BBC Radio-4, presented by legendary jazz trumpeter Humphrey Littleton. Littleton arbitrarily awarded points based on no stated criteria for games that appeared to have neither logical conclusions nor rules. No one knew what the prizes were or why points were awarded— the only real prize for all concerned being an addictive dose of hilarity that somehow commented on much of the nonsense of current events.
5 In my own still-mostly-deductivist classroom we have dumped the textbook as unintelligible, barred points as monsters, and have incorporated self-assessment and words such as “On your way”, “Getting it”, “Almost there”, and “Got it” instead of meaningless points, percentages and letter grades. Verbal in-class contributions count on a par with written assignments. Lower-end students say they get hope. Higher-end students are challenged to demonstrate thinking with their explanations. All students are challenged to demonstrate some learning, that they have improved their understanding. That, at least, is the aim. Some days it works. Some days not.
Wizard math… day 2
Buy this Homage to a Square PiFactory tee-shirt
WE’D LOOKED at the sequence generated when you take a hexagon and steadily add more hexagons. It gives a linear rule. Some students got this easily, others found it challenging.
For 20 minutes the task was to work through a handful of similar problems in the textbook.
The issue was how to give an extension challenge for those who could easily do this sort of problem. Jo Boaler in her What’s Math Got to Do with It?: How Parents and Teachers Can Help Children Learn to Love Their Least Favorite Subject advises open-ended problems are one solution. She also argues that so-called low-ability students benefit from doing hard problems, or, at least listening and eventually participating in finding solutions in mixed-ability group discussion. Talking math is learning maths. The higher ability students benefit by explaining their thinking to other students.
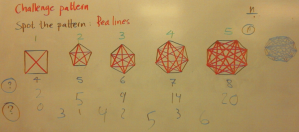On the board I drew a square with diagonals drawn in red, a pentagon with diagonals drawn in red, a hexagon with diagonals, a heptagon and octagon, also with diagonals drawn in red. I also put up an incomplete polygon labelled n. I numbered the polygons 1, 2, 3…
I also wrote: Challenge question, spot patterns, how many red lines?
Breanna was out of her seat immediately counting the lines. Within seconds she announced the number of lines coming from each vertex was the same as the number above the polygon. Then she sat down. So? I asked.
“I can’t do any more,” she replied. I explained she needed to write down her discovery so she had something new to look at and work on to get the next step. No, she said.
Shane was busy counting lines. Rebecca stared at the diagonals in the heptagon and octagon and said it was too complicated. “What about this one,” I said pointing at the pentagon “start here… what you find out here will work for those.”
Breanna had started to build a table. “Breanna,” I said, “tell the others about how you counted the diagonals.”
Shane spotted the number of sides of each polygon was 3 more than the number above the polygon. Breanna explained the number of diagonals was the number of vertices multiplied by the number of lines coming out of one vertex. “And the polygon labelled n?” I coaxed. “The number of sides is n + 3,” said Jonathan from the other side of the room.
Robert who had earlier struggled with the basic exercises, sat watching the board and listening intently to the discussion on Breanna’s table .
As others finished the textbook exercises I drew on the board a 4x4x4 cube made up of 64 small cubes. Next to it I wrote, “if the cube is painted, what proportion of the small cubes have paint on them?”
Stopping the class, I focused everyone on the new problem. On our wall we have a list of Polya’s problem-solving strategies. I pointed to the list with my hand next to “Make it simpler”.
Shane was walking from desk to desk debating with other students the number of cubes. Rebecca asked, “you paint the back too?”
Jonathan and Nick were back and forth at each other, Jonathan slicing out invisible cubes in the air with flattened hands. Nick drew out the net of cube and cut it out: “Look,” he announced, beaming, “I’ve made a cube.”
Jonathan just wanted to explain how he had worked it out, how he got the total number of cubes, how he excluded the cubes inside the large cube, how he decided to not to double count cubes with paint on more than one side… all the time his hands slicing out cubes in the air.
What are the dimensions of the cube? I asked Jonathan. 4 he responded. 4 what? 4 times 4 times 4. How would you write that? 4 to the power three… 4 cubed… Oh! he exclaimed as a giant lightbulb flashed in his brain.
As the students left, Jonathan and Shane were still telling each other about how to solve the problem.
“Do you want to see my work?” said Robert showing me the textbook problem he had completed. “I saw you watching and listening Robert,” I said. Robert smiled.
The Calculus class tries the polygon problem to relax after an intense hour wrestling with implicit differentiation. OK, I say, tell me the number of lines in the 99th polygon.
Becci runs to the board closely followed by Jared. Megan is shouting how to count the lines, but Becci and Jared are engrossed in mathematical disagreement about how to move forward. Josh, Jordan, Jesse and Nicole sketch out the pentagon and hexagon.
Soon the room of nearly 20 students is loudly split between those insisting the rule includes (n −3) and those who say it is (n + 3). As agreement settles on (n + 3), good-natured boasting and mocking ensue.
But, everyone was talking math. And talking math is learning math.
The Pifactory's Weblog 
Recent Comments